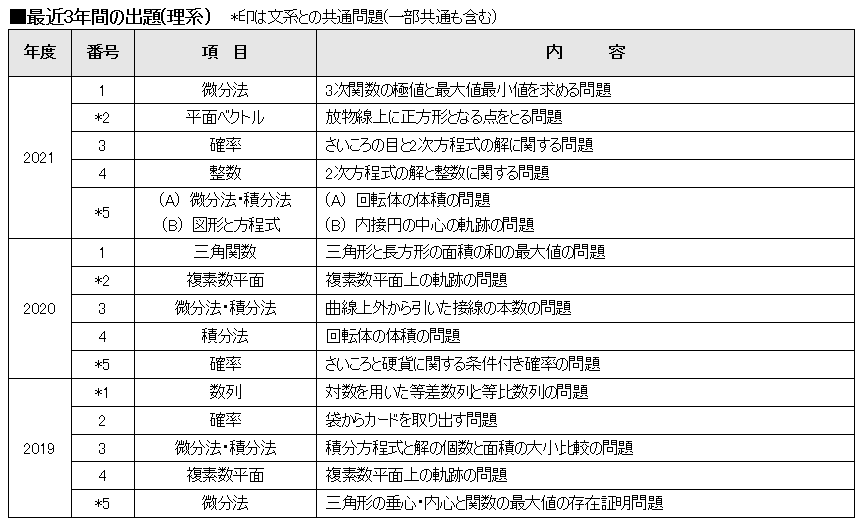
理系は150分で5題。分量は増加したが、難易度は昨年度と変わらなかった。

大問１は3次関数が極値を持つ条件を求めて、最大値と最小値を求める問題であった。計算量が多く、方針を立てられても完答できなかった生徒がいただろう。

大問2はそれぞれの放物線上に正方形となる点をとる問題であった。ベクトルの垂直条件から内積が0を利用すればよかったが、こちらも計算量が多かった。

大問3はさいころの目により2次関数の係数を求める条件つき確率の問題であった。判別式や微分を利用して解けたので、完答したい。

大問4は2次方程式の解と整数の問題であった。有理数と無理数の関係から答えを絞ったり、整数方程式を因数分解したりして、整数解を求めることができた。

大問5は数学Ⅲの範囲で選択問題が出題された。1問目は曲線と直線で囲まれた面積と回転体の体積を求める問題であった。標準的な問題だったので、完答したい。2問目は内接円の中心の軌跡の問題であった。答えが双曲線になったので、図示できるようにもなりたい。

今年はコロナの影響で数学Ⅲからの出題が減り、その代わり計算量が多い問題が出題された。広島大学は融合問題が多いので、さまざまな分野の知識が必要である、例年確率、整数、微分積分の融合問題は多く出題されているので、各分野の標準的な問題は解けるようになっておきたい。

文系は120分で4題。分量は増加し、難易度は昨年度より難化した。

大問1と大問2は理系との共通問題であった。文系にとっては計算量が多かったので、完答できなかったであろう。

大問3は一部理系と同じで、さいころの目により2次関数の係数を求める条件つき確率の問題であった。判別式や微分を利用して解けたので、完答したい。

大問4は三角関数の5倍角の公式を利用する問題であった。2倍角や3倍角を求める方法と同じようにすれば求めることができたので、それを応用できれば解けた。

今年はコロナの影響で例年と比べて計算量の多い問題が出題された。広島大学は融合問題が多く出題されるため、さまざまな分野の知識が必要である。今年は数列の出題がなかったが、確率、数列、ベクトル、微分積分からの多く出題されるので各分野の標準的な問題は解けるようになっておきたい。

鷗州塾高校部については、詳しくはこちら♪

資料請求はこちらから♪来校予約はこちらから♪